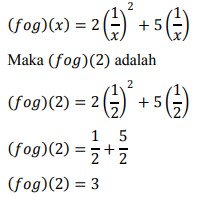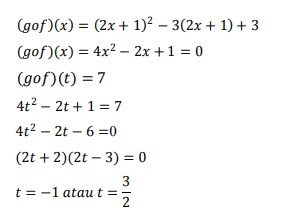SOAL PERSAMAAN DAN PERTIDAKSAMAAN RASIONAL DAN IRASIONAL

Nama: Allisya VIta Dwi Savitri

Kelas: X IPS 1

Absen: 3

Soal Persamaan Rasional

1. Tentukan nilai x yang memenuhi persamaan rasional 

x – 1

2

 – 

3x

4

 = 0

Penyelesaian soal

Untuk menjawab soal ini kita gunakan metode pindah ruas dan kali silang. Ketika memindahkan angka atau variabel dari satu ruas ke ruas lainnya kita ganda negatif menjadi positif atau sebaliknya. Jadi jawaban soal diatas sebagai berikut:

→ 

x – 1

2

 = 

3x

4

→ 4 (x – 1) = 2. 3x
→ 4x – 4 = 6x
→ 4x – 6x = 4
→ -2x = 4
→ x = 

-4

2

 = -2

2. Tentukan nilai x yang memenuhi persamaan rasional dibawah ini.

1 . 

x + 1

x – 2

 = 2
2. 

2x – 4

x + 1

 = 4

Penyelesaian soal

Cara menjawab soal 1 sebagai berikut:

• x + 1 = 2 (x – 2) atau x + 1 = 2x – 4
• x – 2x = -4 – 1
• -x = -5
• x = 5

Cara menjawab soal 2 sebagai berikut:

• 2x – 4 = 4 (x + 1)
• 2x – 4 = 4x + 4
• 2x – 4x = 4 + 4
• -2x = 8
• x = 8/-2 = -4

3. Tentukan nilai x yang memenuhi persamaan rasional berikut.

x – 3

x – 1

 + 

x – 2

x – 1

 = 4

Penyelesaian soal

Cara menjawab soal nomor 3 kita jumlahkan ruas kiri sehingga diperoleh:

→ 

x – 3 + (x – 2)

x – 1

 = 4
→ 

2x – 5

x – 1

 = 4
→ 2x – 5 = 4 (x – 1)
→ 2x – 5 = 4x – 4
→ 4x – 2x = -5 + 4
→ 2x = -1
→ x = -1/2

Soal Pertidaksamaan Rasional

1. Tentukan himpunan penyelesaian dari pertidaksamaan rasional dari 

x – 4

x – 1

 ≥ 0

Penyelesaian soal

Untuk menjawab soal ini tentukan terlebih dahulu syarat pertidaksamaan yaitu x – 1 ≠ 0 atau x ≠ 1.

Selanjutnya kita buat pembuat nol sehingga diperoleh hasil sebagai berikut:

• x – 4 = 0 maka x = 4
• x – 1 = 0 maka x = 1

Kemudian kita buat garis bilangan sebagai berikut:

Untuk menentukan tanda + atau – pada garis bilangan diatas kita ambil satu angka yang lebih kecil dari 1 (misalkan 0). Angka 0 kita subtitusi ke (x – 4)/(x – 1) maka didapat (0 – 4)/(0 – 1) = + 4. Jadi tanda garis bilangan di sebelah kiri 1 adalah + lalu kita buat selang seling untuk tanda garis bilangan selanjutnya.

Karena notasi pertidaksamaan lebih dari sama dengan maka himpunan penyelesaian (x – 4)/(x – 1) terletak pada garis bilangan bertanda + atau pada interval x < 1 atau x ≥ 4.

2. Tentukan himpunan penyelesaian dari pertidaksamaan rasional 

2x + 4

x – 2

 ≺ 0

Penyelesaian soal

Syarat pertidaksamaan soal nomor 2 adalah x – 2 ≠ 0 atau x ≠ 2. Kemudian kita buat pembuat nol sehingga diperoleh:

• 2x + 4 = 0 maka x = -2
• x – 2 = 0 maka x = 2

Karena notasi pertidaksamaan soal ini adalah kurang dari maka interval himpunan penyelesaian berada di tanda negatif atau -2 < x < 2.

3. Tentukan himpunan penyelesaian dari pertidaksamaan rasional 

x2 – 4x + 4

x + 1

 ≺ 0

Penyelesaian soal

Pembilang pada soal diatas kita faktorkan sehingga bentuk soal menjadi:

(x – 2) (x – 2)

x + 1

Syarat yang berlaku pertidaksamaan diatas adalah adalah x + 1 ≠ 0 atau x ≠ -1.

Selanjutnya kita tentukan pembuat nol sebagai berikut:

• (x – 2) (x – 2) = 0 maka diperoleh x = 2.
• x + 1 = 0 maka x = – 1

Selanjutnya kita buat garis bilangan sebagai berikut:

• Untuk x > 2 kita ambil angka 3 lalu subtitusi ke x2 – 4x + 4/x + 1 maka diperoleh 32 – 4 . 3 + 4/3 + 1 = + 1/4. Jadi tanda garis bilangan setelah 2 adalah positif.
• Untuk interval -1 < x < 2 kita angka nol lalu subtitusi seperti poin diatas sehingga didapat 02 – 4 . 0 + 4/0 + 1) = + 4. Jadi tanda garis bilangan diantara – 1 hingga 2 adalah negatif.
• Untuk interval x < -1 kita ambil angka -2 lalu subtitusi seperti 2 poin diatas maka hasilnya – 8. Jadi tanda garis bilangan sebelum -1 adalah negatif. Jika digambarkan seperti dibawah ini.

Jadi interval yang memenuhi adalah x < – 1

Soal persamaan irasional

1. Tentukan nilai x yang memenuhi persamaan irasional √ x – 1   = x – 3

Penyelesaian soal

Untuk menjawab soal 1 kita tentukan dahulu syarat agar persamaan irasional berlaku yaitu:

• x – 1 ≥ 0 atau x ≥ 1.
• x – 3 ≥0 atau x ≥ 3.

Ambil syarat yang terbesar sehingga syarat yang berlaku pada persamaan irasional soal nomor 1 adalah x ≥ 3.

Selanjutnya kita hilangkan tanda akar dengan cara mengkuadratkan kedua ruas persamaan seperti dibawah ini:

• ( √ x – 1 )2 = (x – 3)2
• (x – 1) = x2 – 6x + 9
• x2 – 6x – x + 9 + 1 = 0
• x2 – 7x + 10 = 0
• (x – 2) (x – 5) = 0
• x = 2 atau x = 5

Karena syarat yang berlaku pada persamaan nomor 1 adalah x ≥ 3 maka nilai x yang memenuhi adalah x = 5. Jadi soal nomor 1 jawabannya adalah x = 5.

Untuk memeriksa apakah jawaban ini benar atau salah maka caranya cukup mudah yaitu dengan subtitusi x = 5 ke persamaan irasional nomor 1:

• √ x – 1 = x – 3
• √ 5 – 1 = 5 – 3
• √ 4 = 2
• 2 = 2

Kita lihat jawabannya sesuai.

Jika x = 2 kita subtitusi ke persamaan maka hasilnya sebagai berikut:

• √ 2 – 1 = 2 – 3
• 1 = – 1.

Kita lihat hasilnya tidak sesuai.

2. Tentukan nilai x yang memenuhi persamaan irasional √ x2 – 9   = √ x + 3   .

Penyelesaian soal

Sama seperti nomor 1, kita tentukan dahulu syarat persamaan irasional yaitu:

• x2 – 9 ≥ 0 atau x2 ≥ 9 → x ≤ -3 atau x ≥ 3.
• x + 3 ≥ 0 atau x ≥ -3.

Kita lihat syarat pertama x ≤ -3 dan yang kedua x ≥ -3 jadi syarat yang berlaku adalah x = -3 dan x ≥ 3.

Setelah itu kita kuadratkan kedua ruas persamaan irasional sehingga didapat:

• (√ x2 – 9 )2 = ( √ x + 3 )2.
• x2 – 9 = x + 3
• x2 – x – 9 – 3 = 0
• x2 -x – 12 = 0
• (x – 4) (x + 3) = 0
• x = 4 atau x = -3

Berdasarkan syarat kedua nilai x memenuhi sehingga jawaban soal ini adalah x = – 3 dan x = 4.

Soal Pertidaksamaan Irasional

1. Tentukan himpunan penyelesaian dari pertidaksamaan irasional √ x – 5   < 2.

Penyelesaian soal

Untuk menjawab soal ini kita tentukan terlebih dahulu syarat agar pertidaksamaan irasional berlaku yaitu:

• x – 5 ≥ 0
• x ≥ 5

Selanjutnya kita kuadratkan kedua ruas pertidaksamaan irasional sehingga didapat:

• (√ x – 5 )2 < 22.
• x – 5 < 4
• x < 4 + 5 atau x < 9

Lalu kita buat garis bilangan untuk menentukan irisan antara syarat x ≥ 5 dan x < 9.

Irisan pertidaksamaan irasional nomor 1

Berdasarkan gambar diatas maka himpunan pertidaksamaan irasional nomor 1 adalah 5 ≤ x < 9.

2. Tentukan himpunan penyelesaian dari pertidaksamaan irasional √ x – 1   > 2

Penyelesaian soal

Syarat yang berlaku pada pertidaksamaan irasional diatas sebagai berikut:

• x – 1 ≥ 0.
• x ≥ 1.

Kemudian kita kuadratkan pertidaksamaan diatas sehingga didapat:

• ( √ x – 1 )2 > 22
• x – 1 > 4
• x > 4 + 1
• x > 5

Jadi himpunan penyelesaian pertidaksamaan ini adalah x > 5.

3. Tentukan himpunan penyelesaian dari pertidaksamaan irasional √ 16 – x2   ≤ x + 4.

Penyelesaian soal

Syarat pertidaksamaan irasional:

• 16 – x2 ≥ 0.
• x2 – 16 ≤ 0.
• (x – 4)(x + 4) ≤ 0.
• x = 4 dan x = -4
• -4 ≤ x ≤ 4

Kemudian kita kuadratkan pertidaksamaan seperti dibawah ini:

• ( √ 16 – x2 )2 ≤ (x + 4)2
• 16 – x2 ≤ x2 + 8x + 16
• 16 – x2 – x2 – 8x – 16 ≤ 0
• -2x2 – 8x ≤ 0
• 2x2 + 8x > 0
• 2x (x + 4) > 0
• x ≤ – 4 dan x ≥ 0

Lalu kita buat garis bilangan antara syarat dengan hasil diatas sebagai berikut:

Jadi berdasarkan gambar diatas maka himpunan penyelesaian soal nomor 2 adalah x = -4 dan 0 ≤ x ≤ 4.

Daftar Pustaka 

Judul Postingan: Soal Persamaan Dan Pertidaksamaan Rasional Dan Irasional

Penulis: soalfismat.com

Tahun Posting: Juli 2019

PERSAMAAN DAN PERTIDAKSAMAAN RASIONAL

Nama: Allisya Vita Dwi Savitri

Kelas: X IPS 1

Absen: 3

PERSAMAAN RASIONAL

Persamaan rasional didefinisikan sebagai persamaan suatu pecahan dengan satu atau lebih variabel (x) pada pembilang atau penyebutnya. Sedangkan pertidaksamaan rasional adalah persamaan pecahan dengan notasi kurang dari, lebih dari, kurang dari sama dengan dan lebih dari sama dengan.

Untuk bisa menjawab soal persamaan rasional, kemampuan yang mesti kita miliki adalah perkalian silang dan pindah ruas bilangan. Seperti kita ketahui ketika kita pindah ruas bilangan positif dari kanan ke kiri maka tanda positif menjadi negatif dan sebaliknya.

Cara menentukan penyelesaian persamaan rasional:

1. Nolkan ruas kanan.
2. Faktorkan pembilang dan penyebut.
3. Tentukan syarat penyelesaian yaitu penyebut tidak sama dengan nol.
4. Tentukan penyelesaian yaitu penyebut sama dengan nol dan memenuhi syarat pada langkah 3.
5. Tuliskan HP.

PERTIDAKSAMAAN RASIONAL:

Pertidaksamaan rasional adalah pertidaksamaan yang variabelnya termuat dalam bentuk pecahan.

Contoh Soal:

Daftar Pustaka:

Judul Posting: Persamaan Dan Pertidaksamaan Rasional

Penulis: soalfismat.com, dan catatan matematika

Tahun Posting: Juni 2019 , dan Agustus 2018

PERSAMAAN DAN PERTIDAKSAMAAN IRASIONAL

Nama: Allisya  Vita Dwi Savitri 

Kelas: X IPS 1

Absen: 3

Definisi Persamaan Irasional

Persamaan irasional adalah persamaan yang variabelnya berada di bawah tanda akar dan tidak dapat ditarik keluar tanda akar. Untuk semesta bilangan real, persamaan irasional terdefinisi jika komponen yang memuat variabel di bawah tanda akar bernilai lebih dari atau sama dengan nol.

Langkah Penyelesaian Persamaan Irasional:

1. Syarat terdefinisi yaitu di bawah tanda akar > 0$>>\ge 0$.
2. Solusi (kuadratkan kedua ruas).
3. Tuliskan himpunan penyelesaian (HP).

PERTIDAKSAMAAN IRASIONAL

Pertidaksamaan irasional atau pertidaksamaan bentuk akar adalah pertidaksamaan yang memuat fungsi irasional atau bentuk akar. Pertidaksamaan irasional yang akan dipelajari kali ini adalah pertidaksamaan irasional satu variabel, dimana ada beberapa bentuk umum yang diketahui dari ini, diantaranya :

1. √f(x) < a √f(x) < √g(x)
2. √f(x) ≤ a √f(x) ≤  √g(x)
3. √f(x) > a √f(x)> √g(x)
4. √f(x) ≥ a √f(x) ≥ √g(x)

f (x) dan g (x) adalah fungsi polynomial, f (x), g (x) ≥ 0, a adalah konstanta.

Dalam menentukan himpunan penyelesaian pertidaksamaan irasional yang diubah menjadi pertidaksamaan satu variable ada beberapa sifat yang perlu dipahami antara lain :

jika √f(x) < a dengan f (x) ≥ 0, dan a ≥ 0, maka f (x) <a2

jika √f(x) ≤ a dengan f (x) ≥ 0, dan a ≥ 0, maka f (x) ≤ a2

jika √f(x) > a dengan f (x) ≥ 0, maka f (x) > a2

jika √f(x) ≥ a dengan f (x) ≥ 0, maka f (x) ≥ a2

jika √f(x) < √g(x) dengan f (x), g (x) ≥ 0, maka f (x) < g (x)

jika √f(x) ≤ √g(x) dengan f (x), g (x) ≥ 0, maka f (x) ≤ g (x)

jika √f(x) > √g(x) dengan f (x), g (x) ≥ 0, maka f (x) > g (x)

jika √f(x) ≥ √g(x) dengan f (x), g (x) ≥ 0 maka f (x) ≥ g (x)

Metode Penyelesaian Pertidaksamaan Irasional

Himpunan penyelesaian pertidaksamaan irasional dapat ditentukan dengan langkah-langkah berikut ini :

• Tentukan syarat batas nilai x agar fungsi yang ada di dalam akar terdefinisi.
• Kuadratkan kedua ruas pertidaksamaan sehingga bentuk akar menghilang.
• Tentukan himpunan penyelesaian dari pertidaksamaan yang diperoleh pada langkah 2.
• Gambarkan daerah himpunan penyelesaian yang diperoleh pada langkah 3 dan syarat batas nilai x yang diperoleh pada langkah 1 dalam suatu garis bilangan.
• Tentukan daerah himpunan penyelesaian pertidaksamaan pada langkah 4. daerah himpunan penyelesaian pertidaksamaan irasional adalah daerah yang memuat nilai x yang memenuhi langkah 3 dan 1.

Contoh soal 

Tentukan nilai x yang memenuhi persamaan irasional √ x2 – 9   = √ x + 3   .

Penyelesaian

Tentukan dahulu syarat persamaan irasional yaitu:

• x2 – 9 ≥ 0 atau x2 ≥ 9 → x ≤ -3 atau x ≥ 3.
• x + 3 ≥ 0 atau x ≥ -3.

Kita lihat syarat pertama x ≤ -3 dan yang kedua x ≥ -3 jadi syarat yang berlaku adalah x = -3 dan x ≥ 3.

Setelah itu kita kuadratkan kedua ruas persamaan irasional sehingga didapat:

• (√ x2 – 9 )2 = ( √ x + 3 )2.
• x2 – 9 = x + 3
• x2 – x – 9 – 3 = 0
• x2 -x – 12 = 0
• (x – 4) (x + 3) = 0
• x = 4 atau x = -3

Berdasarkan syarat kedua nilai x memenuhi sehingga jawaban soal ini adalah x = – 3 dan x = 4.

Daftar Pustaka:

Judul Posting: Persamaan Dan tidak Persamaan Irasional

Penulis : catatanmatematika.com, dan materimatematika.com

Tahun Posting: Januari 2021

SOAL KOMPOSISI FUNGSI DAN INVERS FUNGSI

Nama: Allisya Vita Dwi Savitri

Kelas: X IPS 1

Absen: 3

1. Jika f(x) = 3x + 2 dan g(x) = 4x2 . Maka (f o g)(x) dan (g o f)(x) adalah …

Jawab:

(f o g)(x) = f (g(x))

(f o g)(x) = f (4x2)

(f o g)(x) = 3(4x2) + 2

(f o g)(x) = 12x2 + 2

(g o f)(x) = g(f(x))

(g o f)(x) = 4(3x + 2)2

(g o f)(x) = 4(9x2 + 12x + 4)

(g o f)(x) = 36x2 + 48x + 16

Jadi, (f o g)(x) = 12x2 + 2 dan (g o f)(x) = 36x2 + 48x + 16.

2. Diketahui (f o g)(x) = 2x + 4 dan f(x) =x – 2. Tentukan fungsi g (x)!

Jawab:

(f o g)(x) = 2x + 4

f(g(x)) = 2x + 4

g(x) – 2 = 2x + 4

g(x) = 2x + 4 + 2

g(x) = 2x + 6

Jadi, fungsi g (x) adalah g(x) = 2x + 6

3. Tentukan f(x) jika (f o g)(x) = 4x + 6 dan g(x) = 2x + 5.

Jawab:

(f o g)(x) = 4x + 6

f(g(x)) = 4x + 6

f (2x + 5) = 4x + 6

Misal u = 2x + 5, maka x = ½(u-5), sehingga:

f (2x + 5) = 4x + 6

f (u) = 4(½(u-5)) + 6

f (u) = 2u – 10 + 6

f (u) = 2u – 4

f (x) = 2x – 4

Jadi, fungsi f(x) = 2x – 4.

4. Jika f(x) = 2x² + 5x dan g(x) = 1/x maka (fog) (2) adalah …

Jawab:

5. Diketahui fungsi 𝑓(𝑥) = 2𝑥 + 1 dan 𝑔(𝑥) = 𝑥² − 3𝑥 + 3. Jika nilai (𝑔 o f) (𝑡) = 7 maka nilai t adalah …

Jawab:

6. Diberikan dua buah fungsi masing-masing f(x) dan g(x) berturut-turut adalah sebagai berikut :

f(x) = 3x + 2

g(x) = 2 − x

Tentukan:

a) (f o g)(x)

b) (g o f)(x)

Jawab:

a) (f o g)(x)

“Masukkan g(x) nya ke f(x)” sehingga:

(f o g)(x) = f ( g(x) )

= f (2 − x)

= 3(2 − x) + 2

= 6 − 3x + 2

= − 3x + 8

b) (g o f)(x)

“Masukkan f (x) nya ke g (x)” sehingga:

(g o f)(x) = g ( f (x) )

= g ( 3x + 2)

= 2 − ( 3x + 2)

= 2 − 3x − 2

= − 3x

7. Diketahui f(x) = x2 + 1 dan g(x) = 2x − 3, maka (f o g)(x) = ….

Jawab: 

f(x) = x2 + 1

g(x) = 2x − 3

(f o g)(x) =…….?

Masukkan g(x) nya ke f(x)

(f o g)(x) =(2x − 3)2 + 1

(f o g)(x) = 4x2 − 12x + 9 + 1

(f o g)(x) = 4x2 − 12x + 10

8. Diberikan f(x) = 2x + 6, carilah fungsi invers dari f(x) !

Jawab:

f(x) = 2x + 6

y = 2x + 6

2x = y – 6

x = ½y – 3

f-1(x) = ½x – 3

Jadi, fungsi invers dari f(x) adalah f-1(x) = ½x – 3.

9. Jika f(x) = 2x, g(x) = 3x – 1, dan h(x) = x2, maka (f o g o h) (x) adalah …

Jawab:

(f o g o h) (x) = (f o (g o h) (x))

(f o g o h) (x) = f (g (h(x))

(f o g o h) (x) = f (3(x2) – 1)

(f o g o h) (x) = f (3x2 – 1)

(f o g o h) (x) = 2 (3x2 – 1)

(f o g o h) (x) = 6x2 – 2

Jadi, (f o g o h) (x) = 6x2 – 2.

10. Diketahui f(x) = x + 2 dan g(x) = 2x – 4. Tentukan (g o f)-1 (x) !

Jawab:

(g o f)-1 (x) = (f-1 o g-1) (x)

(g o f)-1 (x) = (f-1 (g-1(x))

Tentukan fungsi f-1(x):

f(x) = x + 2

y = x + 2

x = y – 2

f-1(x) = x – 2

Tentukan fungsi g-1(x):

g(x) = 2x – 4

y = 2x – 4

2x = y + 4

x = ½y + 2

g-1(x) = ½x + 2

Substitusikan f-1 (x) dan g-1 (x) ke (g o f)-1 (x) :

(g o f)-1 (x) = (f-1 (g-1(x))

(g o f)-1 (x) = f-1 (½x + 2)

(g o f)-1 (x) = (½x + 2) – 2

(g o f)-1 (x) = ½x

Jadi, (g o f)-1 (x) = ½x.

11. Jika (f o g) (x) = x + 4, dan g(x) = x – 2. Maka carilah invers dari fungsi f(x).

Jawab: 

(f o g) (x) = x + 4

f(g(x)) = x + 4

f(x – 2) = x + 4

Misal u = x – 2, maka x = u + 2, sehingga

f(x – 2) = x + 4

f(u) = u + 2 + 4

f(u) = u + 6

f(x) = x + 6

y = x + 6

x = y – 6

f-1(x) = x – 6

Jadi, invers dari fungsi f(x) adalah f-1(x) = x – 6.

12. Tentukan f⁻¹(x) dari f(x) = 2x + 4

Jawab: 

f(x) = 2x + 4

f(x) – 4 = 2x

13. Tentukan f⁻¹(x) dari 

Jawab:

(7x+3) f(x) = 4x -7

7x f(x) + 3 f(x) = 4x – 7

7x f(x) – 4x = – 3 f(x) – 7

(7 f(x) – 4)x = – 3 f(x) – 7

14. Tentukan f⁻¹(x) dari f(x) = x² – 6x + 15!

Jawab:

f(x) = x² – 6x + 15

f(x) = x² – 6x + 9 – 9 + 15

f(x) = (x-3)² + 6

f(x) – 6 = (x-3)²

15. Tentukan f⁻¹(x) dari f(x) = eˣ⁺⁷!

Jawab:

f(x) = eˣ⁺⁷

ᵉlog f(x) = x + 7

x = ᵉlog f(x) – 7
(karena ᵉlog x = ln x)

f⁻¹(x) = ln x – 7

Daftar Pustaka:

Judul Posting: Soal Komposisi Fungsi Dan Invers Fungsi

Penulis : rumuspintar.com, soalkimia.com, dan zenius.net

Tahun Posting:  17 Maret 2021, 24 Sept 2021, dan 14 Sept 2021