Nama: Allisya Vita Dwi Savitri
Kelas: X IPS 1
Absen: 3
1. Jika f(x) = 3x + 2 dan g(x) = 4x2 . Maka (f o g)(x) dan (g o f)(x) adalah …
Jawab:
(f o g)(x) = f (g(x))
(f o g)(x) = f (4x2)
(f o g)(x) = 3(4x2) + 2
(f o g)(x) = 12x2 + 2
(g o f)(x) = g(f(x))
(g o f)(x) = 4(3x + 2)2
(g o f)(x) = 4(9x2 + 12x + 4)
(g o f)(x) = 36x2 + 48x + 16
Jadi, (f o g)(x) = 12x2 + 2 dan (g o f)(x) = 36x2 + 48x + 16.
2. Diketahui (f o g)(x) = 2x + 4 dan f(x) =x – 2. Tentukan fungsi g (x)!
Jawab:
(f o g)(x) = 2x + 4
f(g(x)) = 2x + 4
g(x) – 2 = 2x + 4
g(x) = 2x + 4 + 2
g(x) = 2x + 6
Jadi, fungsi g (x) adalah g(x) = 2x + 6
3. Tentukan f(x) jika (f o g)(x) = 4x + 6 dan g(x) = 2x + 5.
Jawab:
(f o g)(x) = 4x + 6
f(g(x)) = 4x + 6
f (2x + 5) = 4x + 6
Misal u = 2x + 5, maka x = ½(u-5), sehingga:
f (2x + 5) = 4x + 6
f (u) = 4(½(u-5)) + 6
f (u) = 2u – 10 + 6
f (u) = 2u – 4
f (x) = 2x – 4
Jadi, fungsi f(x) = 2x – 4.
4. Jika f(x) = 2x² + 5x dan g(x) = 1/x maka (fog) (2) adalah …
Jawab:
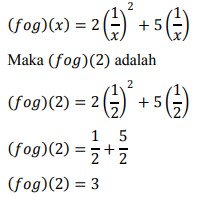
5. Diketahui fungsi 𝑓(𝑥) = 2𝑥 + 1 dan 𝑔(𝑥) = 𝑥² − 3𝑥 + 3. Jika nilai (𝑔 o f) (𝑡) = 7 maka nilai t adalah …
Jawab:
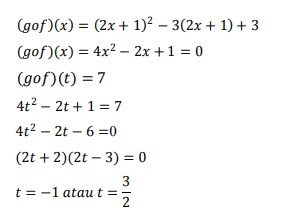
6. Diberikan dua buah fungsi masing-masing f(x) dan g(x) berturut-turut adalah sebagai berikut :
f(x) = 3x + 2
g(x) = 2 − x
Tentukan:
a) (f o g)(x)
b) (g o f)(x)
Jawab:
a) (f o g)(x)
“Masukkan g(x) nya ke f(x)” sehingga:
(f o g)(x) = f ( g(x) )
= f (2 − x)
= 3(2 − x) + 2
= 6 − 3x + 2
= − 3x + 8
b) (g o f)(x)
“Masukkan f (x) nya ke g (x)” sehingga:
(g o f)(x) = g ( f (x) )
= g ( 3x + 2)
= 2 − ( 3x + 2)
= 2 − 3x − 2
= − 3x
7. Diketahui f(x) = x2 + 1 dan g(x) = 2x − 3, maka (f o g)(x) = ….
Jawab:
f(x) = x2 + 1
g(x) = 2x − 3
(f o g)(x) =…….?
Masukkan g(x) nya ke f(x)
(f o g)(x) =(2x − 3)2 + 1
(f o g)(x) = 4x2 − 12x + 9 + 1
(f o g)(x) = 4x2 − 12x + 10
8. Diberikan f(x) = 2x + 6, carilah fungsi invers dari f(x) !
Jawab:
f(x) = 2x + 6
y = 2x + 6
2x = y – 6
x = ½y – 3
f-1(x) = ½x – 3
Jadi, fungsi invers dari f(x) adalah f-1(x) = ½x – 3.
9. Jika f(x) = 2x, g(x) = 3x – 1, dan h(x) = x2, maka (f o g o h) (x) adalah …
Jawab:
(f o g o h) (x) = (f o (g o h) (x))
(f o g o h) (x) = f (g (h(x))
(f o g o h) (x) = f (3(x2) – 1)
(f o g o h) (x) = f (3x2 – 1)
(f o g o h) (x) = 2 (3x2 – 1)
(f o g o h) (x) = 6x2 – 2
Jadi, (f o g o h) (x) = 6x2 – 2.
10. Diketahui f(x) = x + 2 dan g(x) = 2x – 4. Tentukan (g o f)-1 (x) !
Jawab:
(g o f)-1 (x) = (f-1 o g-1) (x)
(g o f)-1 (x) = (f-1 (g-1(x))
Tentukan fungsi f-1(x):
f(x) = x + 2
y = x + 2
x = y – 2
f-1(x) = x – 2
Tentukan fungsi g-1(x):
g(x) = 2x – 4
y = 2x – 4
2x = y + 4
x = ½y + 2
g-1(x) = ½x + 2
Substitusikan f-1 (x) dan g-1 (x) ke (g o f)-1 (x) :
(g o f)-1 (x) = (f-1 (g-1(x))
(g o f)-1 (x) = f-1 (½x + 2)
(g o f)-1 (x) = (½x + 2) – 2
(g o f)-1 (x) = ½x
Jadi, (g o f)-1 (x) = ½x.
11. Jika (f o g) (x) = x + 4, dan g(x) = x – 2. Maka carilah invers dari fungsi f(x).
Jawab:
(f o g) (x) = x + 4
f(g(x)) = x + 4
f(x – 2) = x + 4
Misal u = x – 2, maka x = u + 2, sehingga
f(x – 2) = x + 4
f(u) = u + 2 + 4
f(u) = u + 6
f(x) = x + 6
y = x + 6
x = y – 6
f-1(x) = x – 6
Jadi, invers dari fungsi f(x) adalah f-1(x) = x – 6.
12. Tentukan f⁻¹(x) dari f(x) = 2x + 4
Jawab:
f(x) = 2x + 4
f(x) – 4 = 2x
13. Tentukan f⁻¹(x) dari
Jawab:
(7x+3) f(x) = 4x -7
7x f(x) + 3 f(x) = 4x – 7
7x f(x) – 4x = – 3 f(x) – 7
(7 f(x) – 4)x = – 3 f(x) – 7
14. Tentukan f⁻¹(x) dari f(x) = x² – 6x + 15!
Jawab:
f(x) = x² – 6x + 15
f(x) = x² – 6x + 9 – 9 + 15
f(x) = (x-3)² + 6
f(x) – 6 = (x-3)²
15. Tentukan f⁻¹(x) dari f(x) = eˣ⁺⁷!
Jawab:
f(x) = eˣ⁺⁷
ᵉlog f(x) = x + 7
x = ᵉlog f(x) – 7
(karena ᵉlog x = ln x)
f⁻¹(x) = ln x – 7
Daftar Pustaka:
Judul Posting: Soal Komposisi Fungsi Dan Invers Fungsi
Penulis : rumuspintar.com, soalkimia.com, dan zenius.net
Tahun Posting: 17 Maret 2021, 24 Sept 2021, dan 14 Sept 2021


Tidak ada komentar:
Posting Komentar